Modelling RAFT/emulsion systems provided significant understanding about what mechanisms are important in RAFT/emulsion systems.
Monte Carlo modelling
By considering the possible fates of two radicals and a population of dormant chains in a particle, the applicability of zero-one and pseduo-bulk kinetics can be studied [1].
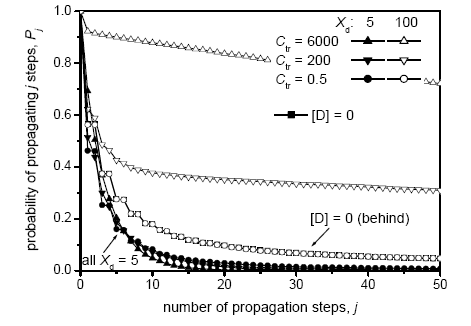
The probability that a given number of monomer units will be consumed in the presence of two radicals gives a measure of the life-time of the radicals in the particles. From this, a suitable average rate coefficient for the termination reaction can be calculated, which may be compared to experimental measures of this quantity [2].
Smith-Ewart population distribution
The Smith-Ewart equations describe the population distribution of radicals in emulsion polymerisations. However, these equations cannot be used in data analysis owing to the complex heirachy involved; reduction to either zero-one or pseudo-bulk kinetics is required for unambiguous determination of the kinetic parameters.
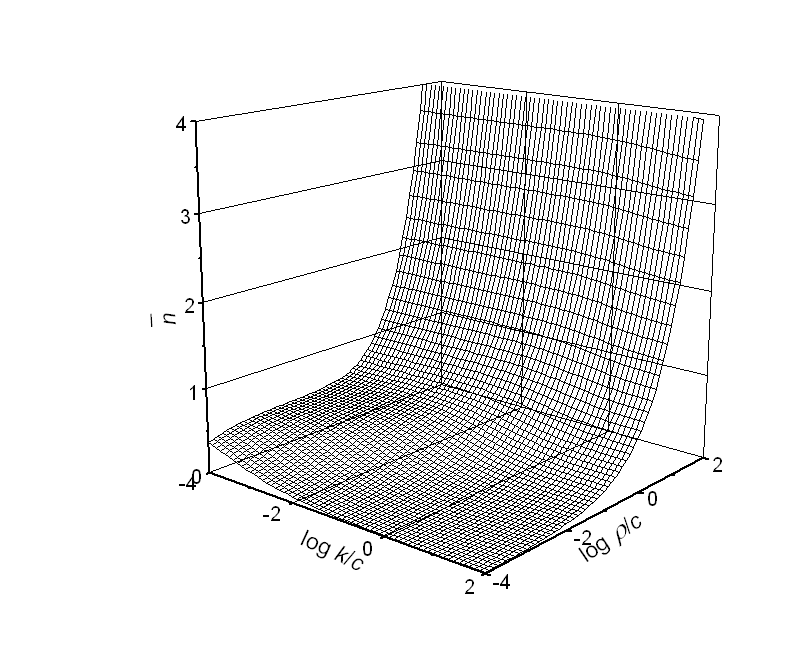
Numerical solution of the steady-state average number of radicals per particle may be readily performed, giving the following surface [3]
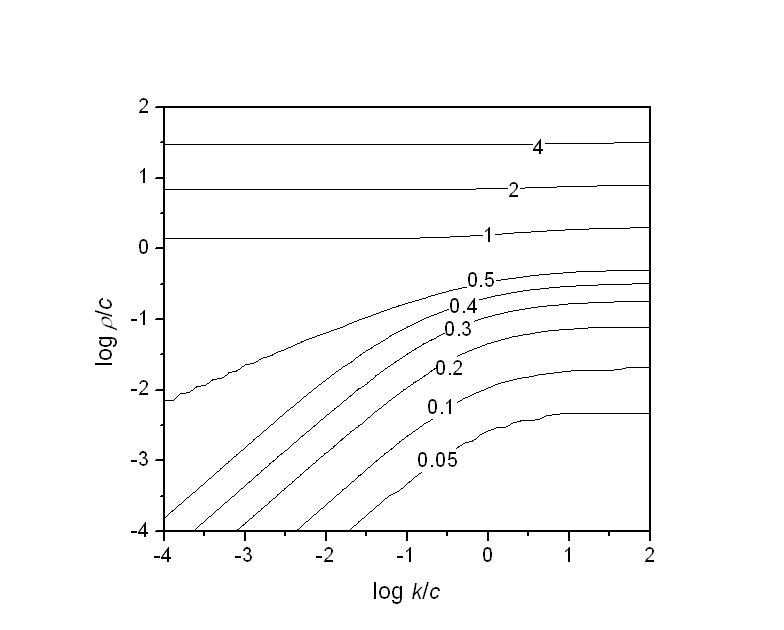
The percentage error between the exact solution of the Smith-Ewart equations and the pseudo-bulk and zero-one approximations may also be calculated.
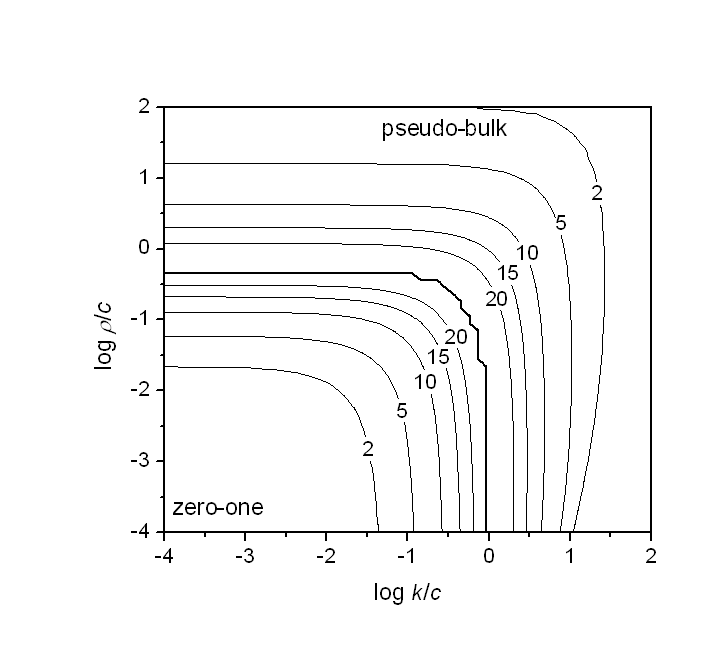
From these calculations, it can be seen that these approximations are applicable to a wide range of real systems with only a small error in the rate of polymerisation.
References
- Chain-length dependence in controlled/living radical polymerizations: physical manifestation and Monte Carlo simulation of reversible transfer agents. SW Prescott. Macromolecules, 36(25), 9608–9621, 2003.
- Radical loss in RAFT-mediated emulsion polymerizations. SW Prescott, MJ Ballard, E Rizzardo and RG Gilbert. Macromolecules, 38(11), 4901–4912, 2005.
- Average termination rate coefficients in emulsion polymerization: effect of compartmentalization on free-radical lifetimes. SW Prescott, MJ Ballard and RG Gilbert. Journal of Polymer Science Part A: Polymer Chemistry, 43(5), 1076–1089, 2005.
Last edited: Tuesday September 9, 2008
Copyright © 1996-2014 Stuart Prescott