The following is the information provided in the program and some screen shots.

                             H3D
 
 A representation of the atomic orbitals of the hydrogen atom.
 
 Stuart Prescott 1996
 
 ================================================
 Using the program (and a bit of Quantum theory):
 
 Firstly, select the orbital which you wish to view. This may be
 done by clicking on the icon corresponding to the name of the
 orbital.
 
 The graphs of the wave (or density) functions passing through
 the maximum in the other two variables are shown. Here,
 theta is the azimuth (angle with the Z-axis) and phi is the co-
 latitude (the angle from the X-axis in the XY-plane).
 
 The surface drawn in the 3D drawing of the orbital is a surface
 of constant wave (or density) function. The value of this
 surface level is shown above the plot and may be changed by
 dragging the horizontal bars that appear on the graph. (Note
 that a surface level of zero cannot generate a surface, so the
 minimum surface level is 10e-7)
 
 The view of the orbital may be rotated using the ArcBall
 which appears in the top left hand corner of the window.
 To use the ArcBall, imagine that the circle represents a
 sphere, and then use the mouse to 'drag' the sphere around.
 The large triangle drawn indicates the axis about which
 the rotation will be performed, and the length of the arc
 corresponds to how much the rotation will be.
 
 To return the orbital to the original viewing position, click
 on the"Reset View" button.To select a new orbital to view,
 click on the "Select Orbital" button.
 
 The "Show Wavefunction"/"Show Density" button changes
 the function displayed by the program. The wave function
 is the representation of Schrodinger's equation, the green
 lobes are where the wavefunction is negative and the red
 lobes are where is is positive. The density function shows
 the probability of finding an electron at any point in space,
 and is the square of the wave function.
 
 ================================================
 Advanced Features:
 
 For those who aren't happy with the quality of the images
 produced by the interpolation (or for those with plenty of
 time on their hands), the size of the interpolation cell
 can be changed.
 
 By clicking with the right mouse button in the vicinity of
 the 3D orbitals, a window is produced allowing the choice of
 interpolation cell sizes.
 
 The smaller the cell size, the more memory is required to do
 the drawing, and the longer will be the time taken to draw
 the 3D representation, but the quality of the image will be
 higher. On some systems, the memory requirement of running
 at a higher resolution will cause memory management faults.
 
 On some orbitals striped or checkerboard patterns may be
 observed. These patterns are due to the interpolation.
 Basically, it comes down to a speed v accuracy issue, and
 speed won.
 
 A cell size of 5 pixels is the default (and recommended) size.
 
 ================================================
 About the development:
 
 This program was written by Stuart Prescott in 1996 as a
 project for the First Year Talented Student Program within
 the Basser Department of Computer Science at the
 University of Sydney. This project was supervised by Dr Ian
 Parkin of the same department. It is both a first program
 in C++, and a first computer graphics application.
 
 The calculation engine used by the program was taken from
 the "H2 Workshop Program" written in FORTRAN by George
 Bacskay and Jeff Reimers, Department of Physical and
 Theoretical Chemistry, University of Sydney.
 
 The ArcBall was developed by Ken Shoemake, Computer
 Graphics Laboratory, University of Pennsylvania, as
 an intuitive, easy-to-use way of rotating objects using
 the computer mouse.
 
 The graphics routines were written using Libsx (The
 Simple X library) version 1.1 - a friendly overlay to the
 Athena Widget Set. Libsx was developed by Dominic
 Giamapolo (dbg@sgi.com) and is available from
 "ftp.x.org/contrib/libraries/libsx.tar.Z"
 
 ================================================
 Copyright (c) Stuart Prescott MCMXCVI
 

The main selection screen

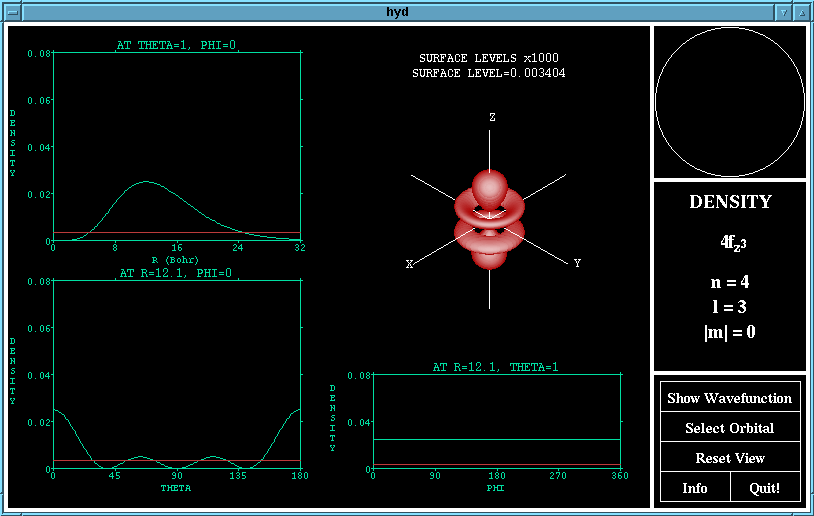
The density function of the 4f_z^3 orbital

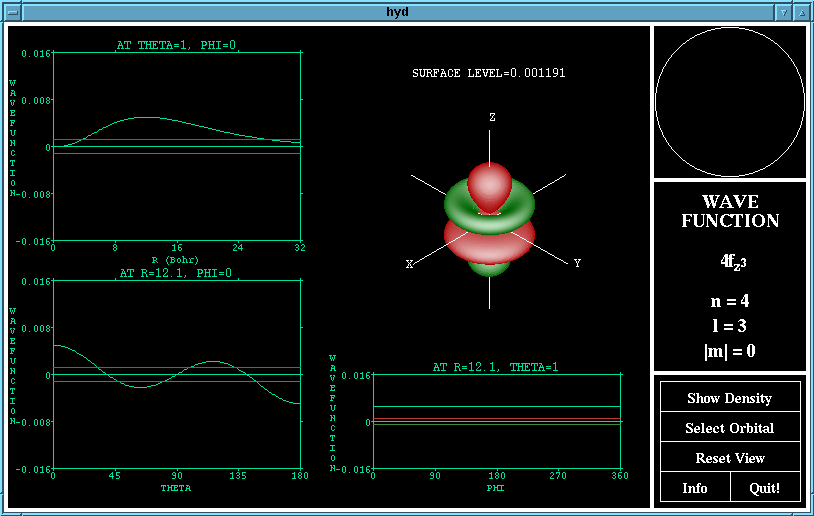
The wave function of the 4f_z^3 orbital

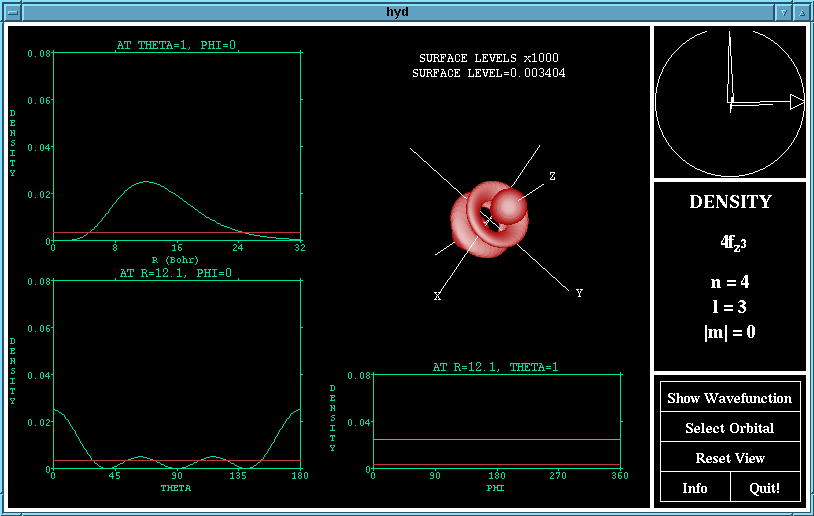
A rotation of the density function of the 4f_z^3 orbital

Other screenshots